多数決は理不尽
過去にもこんな記事を書いているので良かったら見てほしいんですが、日本は選挙をして多数決で国を動かしています。
多数決は多数派の意見が採用されるので多くの人が満足するように仕組み上なっています。
が、当然デメリットもあります。
多数決は実は非常に不平等です。
なぜ不平等かについて前回は解説しているのですが、今回は人気がなくても採用されてしまう多数決のパラドックスについて解説していきます。
多数決のパラドックス

具体的に考える方がわかりやすいので、早速例を出して考えます。
10人でご飯を食べに行く時に多数決で食べたいものを投票して決めたとします。
この時の投票結果は「和食4」「中華3」「イタリアン3」となったとします。
この場合、多数決だと食べたい人が1番多い和食が採用されますね。
しかし、同じ10人で今度は食べたくないものを投票した結果がこうなっていたらどうでしょう。
「和食5」「中華2」「イタリアン3」
この場合、食べたくない人が1番多い和食を多数決で食べに行くのはおかしいですよね?
これが多数決のパラドックスです。
文字だけだとわかりにくいかもしれないので、具体的に表にしてみるとこんな感じです。
| 食べたい | 食べたくない |
| 和食 | 中華 |
| 和食 | 中華 |
| 和食 | イタリアン |
| 和食 | イタリアン |
| 中華 | イタリアン |
| 中華 | 和食 |
| 中華 | 和食 |
| イタリアン | 和食 |
| イタリアン | 和食 |
| イタリアン | 和食 |
この場合、食べたいもので多数決を取る場合でも、食べたくないもので多数決を取る場合でも和食が選ばれるため、1番人気のものを選んだら1番不人気のものになってしまうというパラドックスが発生します。
ちなみに、この1人1票で選びたいものに投票する多数決の方法を単記投票と言います。
選挙はこの単記投票で行われているし、一般的に多数決と言えばこの方式になります。
単記投票以外の多数決
是認投票
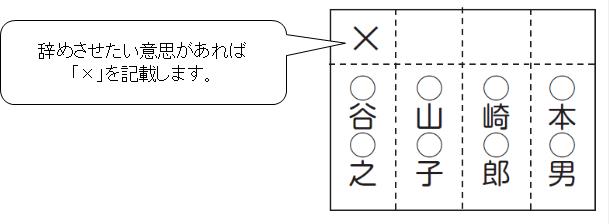
是認投票は採用してもいいと思う候補すべてに投票する多数決の事です。
つまり、単記投票で「和食1」しか入れてない人が、実は和食か中華ならいいと思っていれば「和食1中華1」と投票することになります。
こうすることによって食べたくないものにだけ票が入らなくなるので、1番不人気の選択肢を回避することができます。
さっきの表で考えてみると
| 食べたい | 2番目に食べたい | 食べたくない |
| 和食 | イタリアン | 中華 |
| 和食 | イタリアン | 中華 |
| 和食 | 中華 | イタリアン |
| 和食 | 中華 | イタリアン |
| 中華 | 和食 | イタリアン |
| 中華 | イタリアン | 和食 |
| 中華 | イタリアン | 和食 |
| イタリアン | 中華 | 和食 |
| イタリアン | 中華 | 和食 |
| イタリアン | 中華 | 和食 |
となります。
この場合「中華8」「イタリアン7」「和食5」となるので中華が採用されることになります。(2番目まで全員投票した場合)
こうなるとみんながそれなりに食べたい中華が採用されましたが、当然1番人気だけど1番嫌われている和食は採用されていません。
また、もっと極端な例として、ほぼ全員一致の最高の案を人畜無害な案が凌駕してしまうパラドックスもあります。
例えば、和食、中華、ゲテモノの3つが選択肢だったとします。
そして票が偏っていてこんな投票結果だったとします。
| 食べたい | 2番目に食べたい | 食べたくない |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| 和食 | 中華 | ゲテモノ |
| ゲテモノ | 中華 | 和食 |
つまり、ゲテモノ好きの1人以外は全員和食を1番食べたくて、ゲテモノは絶対に嫌という状態です。
この時2番目に食べたい中華まで全員が投票していると「和食9」「中華10」「ゲテモノ1」となり、1番食べたい人が誰もいない中華が採用されることになります。
ボルダ式得点

ボルダ式得点は、候補すべて順位をつけて下から1点2点…と点数をつけて合計得点を算出する方法です。
こうすることによって1番人気のないものは点数が低く、1番人気のものは点数が高くなるので中途半端なものに順位を取られる心配もありません。
具体的には上の表の場合、「和食28」「中華20」「ゲテモノ12」となるのでちゃんとほとんどの人が食べたい和食が採用されますし、最初の表だったとしても「和食19」「中華21」「イタリアン20」となるので是認投票で採用される中華が採用されました。
ただし、これにも落とし穴があります。
例えば、中華を食べようとしたら店がいっぱいで予約が取れませんでした。
仕方がないので、次に20点で点数の高いイタリアンの店を予約することになるのが普通の流れになります。
しかし、さっきの表から中華を削除した場合の得点を数えてみると
| 1番食べたい | 次点 | 1番食べたくない |
| 和食 | イタリアン | |
| 和食 | イタリアン | |
| 和食 | イタリアン | |
| 和食 | イタリアン | |
| 和食 | イタリアン | |
| イタリアン | 和食 | |
| イタリアン | 和食 | |
| イタリアン | 和食 | |
| イタリアン | 和食 | |
| イタリアン | 和食 |
| 2点 | 1点 |
| 和食 | イタリアン |
| 和食 | イタリアン |
| 和食 | イタリアン |
| 和食 | イタリアン |
| 和食 | イタリアン |
| イタリアン | 和食 |
| イタリアン | 和食 |
| イタリアン | 和食 |
| イタリアン | 和食 |
| イタリアン | 和食 |
このようになって和食とイタリアンが完全に同点になってしまっています。
この時全員が全く意見を変えてはいません。
また、新しくインド料理が選択肢に入った場合はこんな風になるかもしれません。
| 3点 | 2点 | 1点 |
| 和食 | イタリアン | インド料理 |
| 和食 | イタリアン | インド料理 |
| 和食 | イタリアン | インド料理 |
| 和食 | インド料理 | イタリアン |
| 和食 | インド料理 | イタリアン |
| インド料理 | イタリアン | 和食 |
| インド料理 | イタリアン | 和食 |
| イタリアン | 和食 | インド料理 |
| イタリアン | インド料理 | 和食 |
| インド料理 | イタリアン | 和食 |
この場合「和食21」「イタリアン20」「インド料理19」となって和食がイタリアンを逆転します。
2番目だったイタリアンが2つの選択肢での多数決だと同数になるし、無関係な他の選択肢が入って和食とイタリアンの順番は変わらないのに負けることもあるなんて変な話ですよね?
コンドルセ投票

コンドルセ投票は候補すべてを1対1で比べて勝ち負けを付ける方法です。
さっきの表で考えると「和食:中華=4:6」「和食:イタリアン=5:5」「中華:イタリアン=5:5」となります。
| 1番食べたい | 次点 | 1番食べたくない |
| 和食 | イタリアン | 中華 |
| 和食 | イタリアン | 中華 |
| 和食 | 中華 | イタリアン |
| 和食 | 中華 | イタリアン |
| 中華 | 和食 | イタリアン |
| 中華 | イタリアン | 和食 |
| 中華 | イタリアン | 和食 |
| イタリアン | 中華 | 和食 |
| イタリアン | 中華 | 和食 |
| イタリアン | 中華 | 和食 |
つまりこの場合採用するのは中華になります。
ただし、結局中華とイタリアンで比べた場合は同数なのに中華が選ばれているし、単記投票で1番人気の和食はまたしても選ばれていません。
結局おかしい気がしますよね。
さらに、コンドルセ投票にはコンドルセ循環という問題もあります。
コンドルセ循環は勝ち負けがじゃんけんのように循環してしまう結果になる状態のことです。
例えば、和食>イタリアン>中華が4票、イタリアン>中華>和食が3票、中華>和食>イタリアンが3票となっている場合はどうでしょうか?
この場合「和食:中華=4:6」「和食:イタリアン=7:3」「中華:イタリアン=3:7」となります。
こうなると1番人気がどれかもわかりませんし、新しく1人追加したところで一番近い「和食:中華」でも勝敗は変わりません。
アローの不可能性定理
このように色々多数決をなるべく公平にするために考えられた手法はたくさんありますが、ケネス・アローが3つ以上の選択肢から「公正さ」の基準を常に同時に満たすような選好順位選挙制度は設計できない。と証明しました。
これは「アローの不可能性定理」と呼ばれ、ケネス・アローは博士論文で書いたのだとか…
さらに1972年にケネス・アローは「一般的経済均衡理論および厚生理論に対する先駆的貢献を称えて」という理由でノーベル経済学賞を受賞しています。

アローの不可能性定理で言うところの「公正さ」とは以下のものです。
アローの不可能性定理 – Wikipedia
- 人々の選好の順序は自由
- 全ての投票者が選択肢Xを選択肢Yよりも好むとき、集団全体もまたXをYよりも好む(満場一致)
- 独裁者が存在しない。つまり、如何なる個人であれ集団全体の意志を1人で決定することはできない
- 2つの選択肢に関する社会全体の選好順序は、第3の選択肢から影響をうけない
- 社会全体の決定は、堂々巡りの矛盾にならない(a>b , b>cなら必ずa>c)
もちろんこういう公正さを満たさない投票結果がある場合もあるというだけで、実際の多数決はみんなの意見がおおむね一致することが多いです。
これはアロー自身も言っていて、あくまでも特殊な場合にそうなることがあるというだけの話です。
この定理と現実世界の関係については議論がある。アロー自身は「大半の制度は常にうまくいかない訳ではない。私が証明したのは、全てがうまく行かないことが時にはあると言うことだ」と述べている
アローの不可能性定理 – Wikipedia
選挙的にはどうなの?

現在の選挙は単記投票です。
これがなぜ選ばれているか?というと一般的に多数決と言えばこれだからという理由と集計が一番簡単だからという理由でしょう。(調べたわけじゃないので違うかもしれないが…)
今まで基本的にどこの国でも選挙と言えば単記投票なのでこれでもいいのかもしれませんが、この方法だと一番嫌われているところに票が集まっても採用されてしまったなんてことも普通に発生します。
さらに、1番人気のところが当選する見込みがないから他の候補には入れるだけ無駄と思ってしまう可能性も高まります。
そして、いくら嫌われてもとにかく選ばれればいいので炎上商法で目立とうとするバカが発生します。
加えて、組織票で特定の候補を無理やり当選させるというのが一番やりやすいのも単記投票です。
こうやって考えるとデメリットはかなりあると言って良いでしょう。
もちろんデメリットだけでなく、開票が簡単、一番人気が選ばれる、候補者を選ぶ労力が一番少ないといったメリットもあります。
結局のところ、デメリットは非常に大きいと僕は思いますが、手間の観点からメリットも非常に大きいので多分今後もこのまま単記投票で変わらないんだと思います。
一番現実的な方法は、単記投票で一番当選してほしい候補と一緒に一番当選してほしくない候補も書くとかですかね?
ただ、そういった変更を選挙で勝っている人たちがするわけがないですし、間違って逆に書く人もいるみたいなバカすぎる理由でやっぱり無理でしょうね。
最後のまとめ
今回は「【パラドックス】多数決で一番不人気でも選ばれる」というタイトルで多数決のパラドックスについて説明をしました。
日本は選挙をして多数決で国を動かしています。が、今回は人気がなくても採用されてしまう多数決のパラドックスについて解説しています。
一般的な多数決は単記投票という方式で、1人1票が1番だと思う候補に対して投票をします。
これは、複数の候補がいる場合当選した候補が実は1番嫌われている不人気の候補となる可能性がある投票システムです。
このパラドックスを解消するために様々な多数決の方法が考えられました。
例えば、1番だけでなく合格の候補に1票ずつ入れる「是認投票」、1位から最下位まで順番を付けて点数を振る「ボルダ式得点」、1対1で勝ち負けを決める「コンドルセ投票」なんかがあります。
しかし、アメリカの経済学者ケネス・アローによって3つ以上の候補がある場合に5つの「公正さ」の基準を常に同時に満たすような選好順位選挙制度は設計できない。ということが証明されます。
あくまでも全てがうまく行かないことが時にはあるという話ですが、多数決は結果によっては民意を反映しないということが証明されているとも言えます。
これを踏まえて選挙で単記投票をすることの是非を考えると、メリットは
- 開票が簡単
- 一番人気が選ばれる
- 候補者を選ぶ労力が一番少ない
デメリットは
- 一番不人気が選ばれることもある
- 他の候補に入れるだけ無駄となってしまう場合がある
- 選ばれればいいので嫌われても問題ない炎上商法が有利
- 組織票で特定の候補を無理やり当選させるのが一番やりやすい
と言った感じです。
開票のしやすさ、ルールを変える権利を今の選挙ルールで勝っている人たちが持っているといった理由から変わることはないでしょうね…
ちなみに選挙で言うと「白票」で検索すると上の方にこんなのが出てくるんですが、千葉の現職知事が過去にこんなことを言っていて、結局政治家は民衆の事なんかどうでもよくて、選挙で勝てるかどうかしか気にしていません。(本当に民衆全員のことを考えているなら選挙活動に参加していない人のことも考えないとおかしい)
うんこしかないレストランで注文なんかしないんですけどね…
結局のところやっぱり選挙は茶番となってしまうのがつらいところです。
とは言え、こんな言われたらあたり前の事でもほとんどの国民は理解せず(させず)に選挙をかなりの期間続けているんだから民主主義国家って何なんでしょうね…
別に独裁政治や社会主義はもっと嫌なのであれですが、なんかもっといい方法ないんですかね…
とりあえず現状できることは、みんながちゃんとした知識を持って考えて候補者を選ぶことだと思います。
こんな記事も書いてます。





コメント