継続率と連荘数の関係
ぱちんこやスロットで継続率○○%ループとか実質継続率○○%みたいな表記をよく見ることがあると思います。
継続率だと80%なら100回試行すれば80回が継続するという当たり前なことなんですが、じゃあ継続率80%はどれくらいの連荘が期待できるでしょうか?
80%だと難しいなら100%なら?50%ならどうでしょうか?
今回は継続率からどれくらいの期待連荘数があるのか?と○○回連荘する確率はどれくらいあるのか?を計算する方法を解説します。
ついでに例として、スマスロ北斗の継続率を計算してみます。
期待連荘回数の計算
上で書いた80%の期待連荘回数は5回なんですが当たっていましたか?
ちなみに100%なら当然∞回、50%なら2回となります。
まあものすごく厳密な話をすると閉店取り切れずやコンプリート機能の話があるので、ぱちんこパチスロで考える場合は本当にごくわずかに計算上の期待回数よりも少なくなるんですが…
そんなことは置いといて、この期待連荘回数の計算方法は簡単なパターンと難しいパターンがあります。
ぶっちゃけほとんどの場合で簡単なパターンで計算するだけでいい気もするので、今回はとりあえずどちらの方法も解説します。
簡単な計算
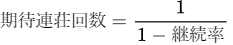
この時の継続率は80%なら0.8です。
つまり継続率80%の場合は、1/(1-0.8)で1/0.2=5となるので期待連荘回数は5回となります。
この計算式だと継続率100%は0割りになるので計算できないですが、やってる計算はlimみたいなもんなので無限に近づいていくので感覚的にも分かるでしょう。
ただしこれだと期待連荘回数は分かりますが、ピッタリ期待通りの連荘回数になるのは何%なのか?
○○連したけどこれってどれくらい珍しいことなんだろう?
みたいな疑問に全く答えられません。
そういった小難しいことを考える場合は難しい方のパターンを使用する必要があります。
難しい計算
指定の連荘回数で連荘終了する確率は以下の式で求められます。

この時、n=1の場合は単純に1回非当せん確率を計算すればいいだけで(n-1)回当せん確率は無視していいことになります。
この計算ができれば各連荘数で終了する確率が分かるのでn回まで連荘する確率はn-1回までに連荘する確率をすべて足した確率を1から引けばいいとなるわけです。
文章で書かれると微妙にわかりにくいかもしれないですが、計算式だとこんな感じです。
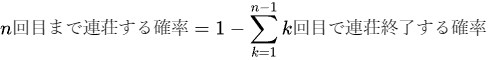
ざっくり例を出すと継続率80%で単発終了する確率は1-0.8=0.2ですが、2連終了の確率は0.8*0.2=0.16となり、3連終了の確率は0.8^2*0.2=0.128となります。
なので4回目まで連荘する確率は1-(0.2+0.16+0.128)=0.512と計算することができます。
スマスロ北斗の連荘確率

計算するうえでの前提条件があるのでまずは羅列しておきます。
- Vストック非考慮(ストックしない)
- 無想転生非考慮(突入しない)
要するに最低限の継続率です。
前提条件を踏まえたうえでの各継続率別の連荘確率はこんな感じになります。
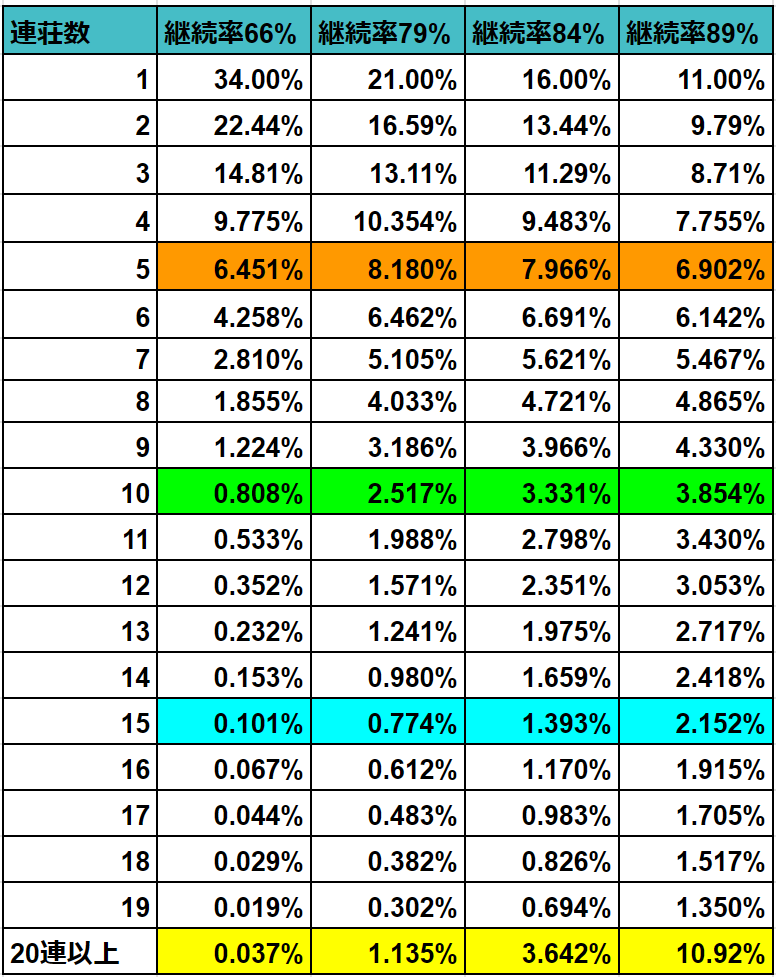
計算式自体は解説しているので別に話すこともないです。
平均連荘数はサクッと計算できるのであれですが、計算するとこんな感じです。(上段は簡単計算、下段は20連打ち止めで難しい計算)

簡単な計算は∞回なので理論値ですが、難しい方の計算は20連以上を全部20連で計算しているのでだいぶ誤差が出ていますね…
GAPOLIのバラエティ北斗
継続率が出たのでざっくりとGAPOLIのバラエティ北斗でどうなるのかを当てはめていきます。
なおBB継続率はいったんこれを使います。
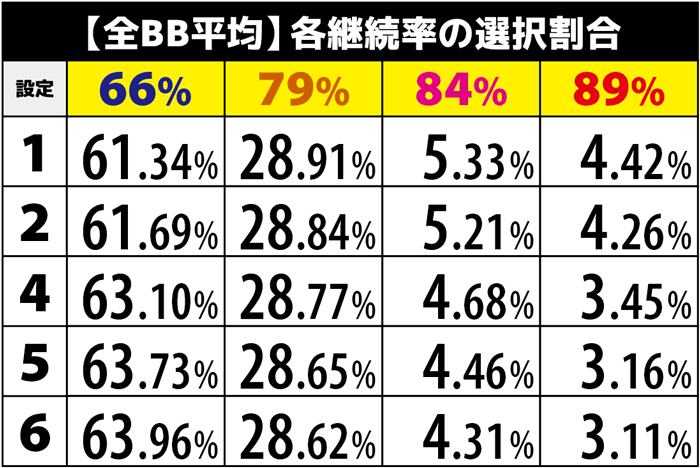
これは天井とかが含まれているのでたぶん普通に当たった場合よりも甘いんですが、これしか見つからないのでまずはこれで計算します。
計算した結果がこんな感じです。
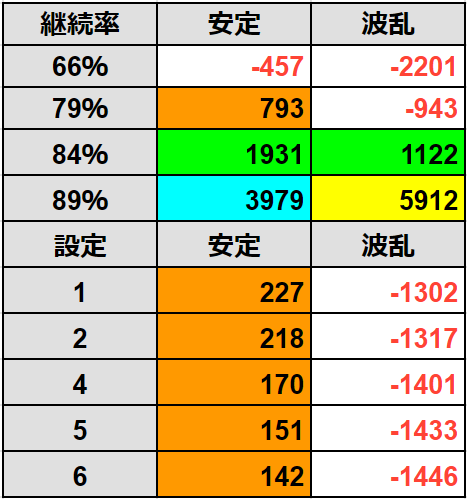
安定は全部の設定でプラス、波乱は全部の設定でマイナスとなりました。
まあ波乱がマイナスなのは前提条件の「Vストック非考慮」と「無想転生非考慮」がでかすぎるのでわかるんですが、逆に言うとこの前提条件でも安定はプラスになるのだからなかなか驚きの結果です。
とは言え、上で使った全BB平均は計算前に説明を入れたように天井での北斗揃いとかが含まれているので鵜呑みにして使うわけにもいきません。
一応北斗揃いの時の継続率は出ているのでこれを参考程度に継続率がどの程度まで悪くてもプラスになるのかを適当に考えていきます。(本当は斜め揃い系の66%否定もあるけど面倒なのでフィーリングでやる)
とりあえずこんな感じの条件にするとどうなるかを計算しました。
- 天井到達率の一番低そうな継続率の一番悪い設定6をベースに考える
- 89%継続は北斗揃いでしか当せんしない
- 北斗揃い確率は1%
- 89%継続が0.5%になるように89%継続の振り分けを引き下げ
- 84%継続を89%継続で引き下げた分の1/2で引き下げ
- 引き下げた分の差分を66%継続と79%継続に63.96:28.62で振り分け
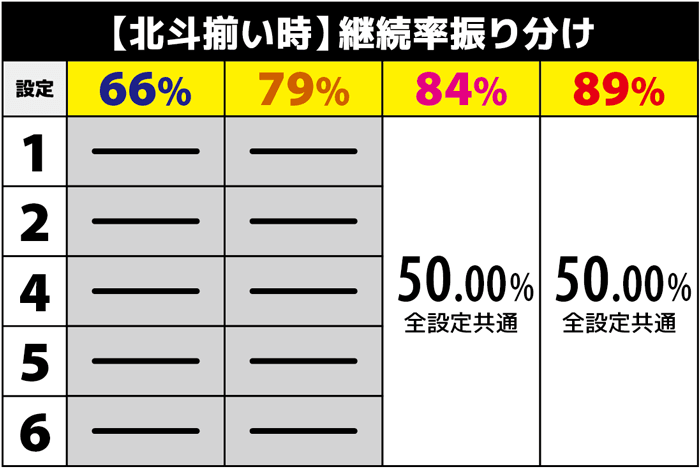
条件を見てもピンとこないと思うので表にするとこんな感じです。
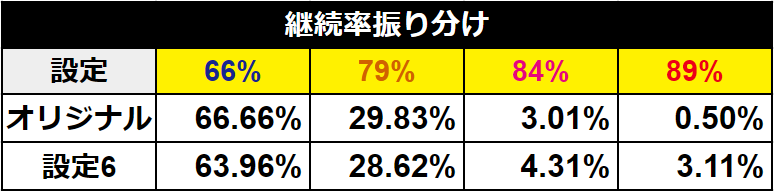
66%継続が約66.7%(約2/3)で約30%が79%継続、約3%が84%継続で89%継続は0.5%となります。
89%継続の振り分けをおそらく普通よりも十分に絞った気がするので、めちゃくちゃ厳しい条件にしたつもりですしこれでプラスなら十分打てるラインだと言えるんじゃないでしょうか?
と言うかそもそも前提条件の「Vストック非考慮」と「無想転生非考慮」を踏まえれば少々のマイナス程度なら十分プラスだと思いますが。
で、計算した結果はこんな感じです。

打てるんですねえ…
さすがにこれ以上振り分けが悪いってことはなさそうな気はするし、Vストックと無想転生を考慮するともっと甘いので、実はバラエティ北斗はかなりの激甘台なのかもしれません。
そんなわけでイベント対象でもないバラエティ北斗を約200回くらい安定で回してみましたが、普通にドマイナスで終わりました。
200回くらいじゃ全然確率が収束するわけもないですし、そもそも統計的に有意な値すら取れないくらいの回数ですが、回すのもサンプルを集めるのも非常に面倒なので多分もう僕は通常営業時にはやらないです。
統計的に有意な数のサンプルを集計できた方がいたら結果を教えてください。
なお、ドマイナスで終わりましたが、1セット目の突破率は40回オーバーで80%越えとなっていたので引き自体はそんなに悪いわけではないと思うんですが…
と言うか無想転生を考慮すると継続率は連荘数を重ねるごとに高くなる気がするんですけど…
あと何度か書いていますが、波乱の期待値がめちゃくちゃマイナスに振り切っているのはVストックと無想転生の恩恵がないからです。
波乱の方が実際はもっと期待値が出る可能性は十分にあります。
最後のまとめ
今回は「【GAPOLI】スマスロ北斗の継続率と連荘数について」と言うタイトルで期待連荘回数の計算方法とスマスロ北斗の期待連荘回数、そしてその計算をもとにGAPOLIのバラエティ北斗の期待値計算をしました。
期待連荘回数の計算は基本的には以下の通りです。
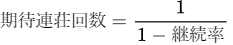
指定の連荘回数で連荘終了する確率は以下の式で求められます。

n回目で連荘終了する確率を求めることで以下のように期待連荘回数を求めることもできます。
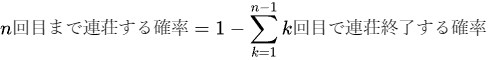
これらを基にスマスロ北斗の継続率別に計算した結果を表にして上に置いておきました。
また、指定の連荘回数で連荘終了する確率が計算できたのでGAPOLIのバラエティ北斗の期待値も計算しました。
前提条件がガバいのであれですが、かなり高めの値になったので参考程度に使ってみてください。
まあ期待値プラスっぽいのに実際に打ってみたら普通にマイナスくらったし面倒なのであまり積極的にオススメはしませんが。
こんな記事も書いています。





コメント